深度优先搜索维基百科 百度百科
深度优先搜索算法(英语:Depth-First-Search,简称DFS)是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
深度优先遍历图的方法是,从图中某顶点v出发:
(1)访问顶点v;
(2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
广度优先搜索维基百科 百度百科
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
广(宽度)度优先搜索使用队列(queue)来实现,可以看做一个倒立的树形:
1、把根节点放到队列的末尾。
2、每次从队列的头部取出一个元素,查看这个元素所有的下一级元素,把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。
3、找到所要找的元素时结束程序。
4、如果遍历整个树还没有找到,结束程序。
以下程序基于图:
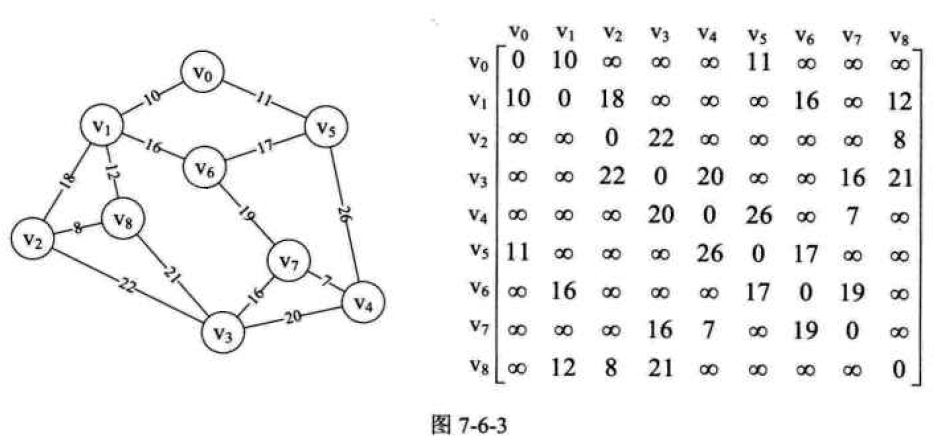
代码:
import java.util.LinkedList;
public class Graph {
private int vertexSize;// 顶点数量
private int[] vertexes;// 顶点数组
private int[][] matrix;// 矩阵
private final static int MAX_WEIGHT = 1000;
private boolean[] isVisited;
public Graph(int vertexSize) {
this.vertexSize = vertexSize;
// 初始化矩阵
matrix = new int[vertexSize][vertexSize];
// 顶点数组初始化
vertexes = new int[vertexSize];
for (int i = 0; i < vertexSize; i++) {
vertexes[i] = i;
}
// 是否访问初始化
isVisited = new boolean[vertexSize];
}
// 获得顶点的出度
public int getOutDegree(int index) {
int degree = 0;
for (int j = 0; j < matrix[index].length; j++) {
int weight = matrix[index][j];
if (weight != MAX_WEIGHT && weight != 0) {
degree++;
}
}
return degree;
}
// 获得顶点的入度
public int getInDegree(int index) {
int degree = 0;
for (int j = 0; j < matrix[index].length; j++) {
int weight = matrix[j][index];
if (weight != MAX_WEIGHT && weight != 0) {
degree++;
}
}
return degree;
}
// 获取两个点之间的权值
public int getWeight(int v1, int v2) {
int weight = matrix[v1][v2];
return weight == 0 ? 0 : (weight == MAX_WEIGHT ? -1 : weight);
}
/**
* 获取某个顶点的第一个邻接点
*
* @param index
* @return
*/ public int getFirstNeighbor(int index) {
for (int j = 0; j < vertexSize; j++) {
if (matrix[index][j] > 0 && matrix[index][j] < MAX_WEIGHT) {
return j;
}
}
return -1;
}
/**
* 根据前一个邻接点的下标取得下一个邻接点 v1 要找的点 v2 表示该节点相对于哪个邻接点去获取下一个邻接点
*
* @return
*/ public int getNextNeighbor(int v1, int index) {
for (int j = index + 1; j < vertexSize; j++) {
if (matrix[v1][j] > 0 && matrix[v1][j] < MAX_WEIGHT) {
return j;
}
}
return -1;
}
/**
* 图的深度优先遍历
*
* @return
*/ private void depthFirstSearch(int i) {
isVisited[i] = true;
int w = getFirstNeighbor(i);
while (w != -1) {
if (!isVisited[w]) {
System.out.println("访问到了:" + w + "顶点");
depthFirstSearch(w);
}
w = getNextNeighbor(i, w);// 第一个相对于w的邻接点
}
}
/**
* 对外公开的图的深度优先遍历 DFS
*
* @return
*/ public void depthFirstSearch() {
isVisited = new boolean[vertexSize];
for (int i = 0; i < vertexSize; i++) {
if (!isVisited[i]) {
System.out.println("访问到了:" + i + "顶点");
depthFirstSearch(i);
}
}
isVisited = new boolean[vertexSize];
}
/**
* 对外公开的图的广度优先搜索算法 BFS
*
* @return
*/ public void broadFirstSearch() {
isVisited = new boolean[vertexSize];
for (int i = 0; i < vertexSize; i++) {
if (!isVisited[i]) {
broadFirstSearch(i);
}
}
}
private void broadFirstSearch(int i) {
int u, w;// u 队列中的节点 w后面的邻阶顶点
LinkedList<Integer> queue = new LinkedList<Integer>();
System.out.println("访问到:" + i + "顶点");
isVisited[i] = true;
queue.add(i);// 第一次把v0加到队列
while (!queue.isEmpty()) {
u = queue.removeFirst();
w = getFirstNeighbor(u);
while (w != -1) {
if (!isVisited[w]) {
System.out.println("访问到了:" + w + "顶点");
isVisited[w] = true;
queue.add(w);
}
w = getNextNeighbor(u, w);
}
}
}
public int[][] getMatrix() {
return matrix;
}
public void setMatrix(int[][] matrix) {
this.matrix = matrix;
}
public static void main(String[] args) {
// Graph graph = new Graph(5);
// int[] a1 = new int[]{0, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 6};
// int[] a2 = new int[]{9, 0, 3, MAX_WEIGHT, MAX_WEIGHT};
// int[] a3 = new int[]{2, MAX_WEIGHT, 0, 5, MAX_WEIGHT};
// int[] a4 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0, 1};
// int[] a5 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0};
// graph.matrix[0] = a1;
// graph.matrix[1] = a2;
// graph.matrix[2] = a3;
// graph.matrix[3] = a4;
// graph.matrix[4] = a5;
// System.out.println("V0的出度:"+graph.getOutDegree(0));
// System.out.println("V0的入度:"+graph.getInDegree(0));
// System.out.println("V0到V4的权值:"+graph.getWeight(0,4));
Graph graph = new Graph(9);
int[] a1 = new int[] { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] a2 = new int[] { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12 };
int[] a3 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8 };
int[] a4 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21 };
int[] a5 = new int[] { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT };
int[] a6 = new int[] { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT };
int[] a7 = new int[] { MAX_WEIGHT, 16, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
int[] a8 = new int[] { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT };
int[] a9 = new int[] { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 };
graph.matrix[0] = a1;
graph.matrix[1] = a2;
graph.matrix[2] = a3;
graph.matrix[3] = a4;
graph.matrix[4] = a5;
graph.matrix[5] = a6;
graph.matrix[6] = a7;
graph.matrix[7] = a8;
graph.matrix[8] = a9;
// graph.depthFirstSearch();
graph.broadFirstSearch();
}
} 本站由以下主机服务商提供服务支持:
0条评论